Signal extension modes#

Because the most common and practical way of representing digital signals in computer science is with finite arrays of values, some extrapolation of the input data has to be performed in order to extend the signal before computing the Discrete Wavelet Transform using the cascading filter banks algorithm.

Depending on the extrapolation method, significant artifacts at the signal’s borders can be introduced during that process, which in turn may lead to inaccurate computations of the DWT at the signal’s ends.

PyWavelets provides several methods of signal extrapolation that can be used to minimize this negative effect:

zero - zero-padding - signal is extended by adding zero samples:
```
... 0  0 | x1 x2 ... xn | 0  0 ...
```

constant - constant-padding - border values are replicated:
```
... x1 x1 | x1 x2 ... xn | xn xn ...
```

symmetric - symmetric-padding - signal is extended by mirroring samples. This mode is also known as half-sample symmetric.:
```
... x2 x1 | x1 x2 ... xn | xn xn-1 ...
```

reflect - reflect-padding - signal is extended by reflecting samples. This mode is also known as whole-sample symmetric.:
```
... x3 x2 | x1 x2 ... xn | xn-1 xn-2 ...
```

periodic - periodic-padding - signal is treated as a periodic one:
```
... xn-1 xn | x1 x2 ... xn | x1 x2 ...
```

smooth - smooth-padding - signal is extended according to the first derivatives calculated on the edges (straight line)

antisymmetric - anti-symmetric padding - signal is extended by mirroring and negating samples. This mode is also known as half-sample anti-symmetric:
```
... -x2 -x1 | x1 x2 ... xn | -xn -xn-1 ...
```

antireflect - anti-symmetric-reflect padding - signal is extended by reflecting anti-symmetrically about the edge samples. This mode is also known as whole-sample anti-symmetric:
```
... (2*x1 - x3) (2*x1 - x2) | x1 x2 ... xn | (2*xn - xn-1) (2*xn - xn-2) ...
```

DWT performed for these extension modes is slightly redundant, but ensures perfect reconstruction. To receive the smallest possible number of coefficients, computations can be performed with the periodization mode:

periodization - periodization - is like periodic-padding but gives the smallest possible number of decomposition coefficients. IDWT must be performed with the same mode.

Example:

>>> import pywt
>>> print(pywt.Modes.modes)
['zero', 'constant', 'symmetric', 'periodic', 'smooth', 'periodization', 'reflect', 'antisymmetric', 'antireflect']

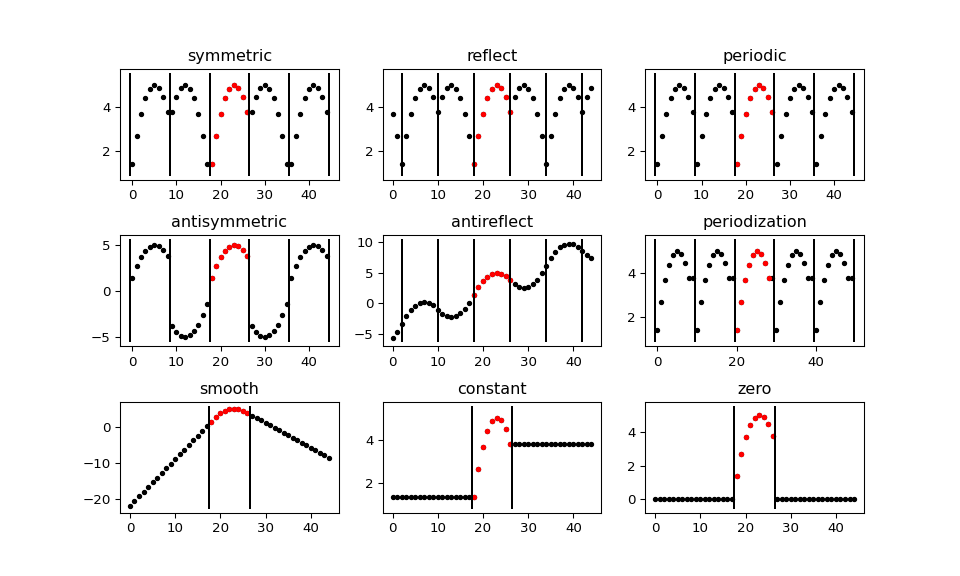
The following figure illustrates how a short signal (red) gets extended (black) outside of its original extent. Note that periodization first extends the signal to an even length prior to using periodic boundary conditions.

"""A visual illustration of the various signal extension modes supported in
PyWavelets. For efficiency, in the C routines the array is not actually
extended as is done here. This is just a demo for easier visual explanation of
the behavior of the various boundary modes.

In practice, which signal extension mode is beneficial will depend on the
signal characteristics.  For this particular signal, some modes such as
"periodic",  "antisymmetric" and "zero" result in large discontinuities that
would lead to large amplitude boundary coefficients in the detail coefficients
of a discrete wavelet transform.
"""
import numpy as np
from matplotlib import pyplot as plt

from pywt._doc_utils import boundary_mode_subplot

# synthetic test signal
x = 5 - np.linspace(-1.9, 1.1, 9)**2

# Create a figure with one subplots per boundary mode
fig, axes = plt.subplots(3, 3, figsize=(10, 6))
plt.subplots_adjust(hspace=0.5)
axes = axes.ravel()
boundary_mode_subplot(x, 'symmetric', axes[0], symw=False)
boundary_mode_subplot(x, 'reflect', axes[1], symw=True)
boundary_mode_subplot(x, 'periodic', axes[2], symw=False)
boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False)
boundary_mode_subplot(x, 'antireflect', axes[4], symw=True)
boundary_mode_subplot(x, 'periodization', axes[5], symw=False)
boundary_mode_subplot(x, 'smooth', axes[6], symw=False)
boundary_mode_subplot(x, 'constant', axes[7], symw=False)
boundary_mode_subplot(x, 'zero', axes[8], symw=False)
plt.show()

Notice that you can use any of the following ways of passing wavelet and mode parameters:

>>> import pywt
>>> (a, d) = pywt.dwt([1,2,3,4,5,6], 'db2', 'smooth')
>>> (a, d) = pywt.dwt([1,2,3,4,5,6], pywt.Wavelet('db2'), pywt.Modes.smooth)

Note

Extending data in context of PyWavelets does not mean reallocation of the data in the computer’s physical memory and copying values, but rather computing the extra values only when they are needed. This feature saves extra memory and CPU resources and helps to avoid page swapping when handling relatively big data arrays on computers with low physical memory.

Naming Conventions#

The correspondence between PyWavelets edge modes and the extension modes available in Matlab’s dwtmode and numpy’s pad are tabulated here for reference.

PyWavelets	Matlab	numpy.pad
symmetric	sym, symh	symmetric
reflect	symw	reflect
smooth	spd, sp1	N/A
constant	sp0	edge
zero	zpd	constant, cval=0
periodic	ppd	wrap
periodization	per	N/A
antisymmetric	asym, asymh	N/A
antireflect	asymw	reflect, reflect_type=’odd’

Padding using PyWavelets Signal Extension Modes - `pad`#

pywt.pad(x, pad_widths, mode)#

Extend a 1D signal using a given boundary mode.

This function operates like numpy.pad() but supports all signal extension modes that can be used by PyWavelets discrete wavelet transforms.

Parameters

xndarray: The array to pad
pad_widths{sequence, array_like, int}: Number of values padded to the edges of each axis. ((before_1, after_1), … (before_N, after_N)) unique pad widths for each axis. ((before, after),) yields same before and after pad for each axis. (pad,) or int is a shortcut for before = after = pad width for all axes.
modestr, optional: Signal extension mode, see Modes.

Returns

padndarray: Padded array of rank equal to array with shape increased according to pad_widths.

Notes

The performance of padding in dimensions > 1 may be substantially slower for modes 'smooth' and 'antisymmetric' as these modes are not supported efficiently by the underlying numpy.pad() function.

Note that the behavior of the 'constant' mode here follows the PyWavelets convention which is different from NumPy (it is equivalent to mode='edge' in numpy.pad()).

Pywavelets provides a function, pad(), that operates like numpy.pad(), but supports the PyWavelets signal extension modes discussed above. For efficiency, the DWT routines in PyWavelets do not expclitly create padded signals using this function. It can be used to manually prepad signals to reduce boundary effects in functions such as cwt() and swt() that do not currently support all of these signal extension modes.

Signal extension modes#

Naming Conventions#

Padding using PyWavelets Signal Extension Modes - pad#

Padding using PyWavelets Signal Extension Modes - `pad`#