Thresholding functions#
The thresholding helper module implements the most popular signal
thresholding functions.
Thresholding#
- pywt.threshold(data, value, mode='soft', substitute=0)#
Thresholds the input data depending on the mode argument.
In
softthresholding [1], data values with absolute value less than param are replaced with substitute. Data values with absolute value greater or equal to the thresholding value are shrunk toward zero by value. In other words, the new value isdata/np.abs(data) * np.maximum(np.abs(data) - value, 0).In
hardthresholding, the data values where their absolute value is less than the value param are replaced with substitute. Data values with absolute value greater or equal to the thresholding value stay untouched.garrotecorresponds to the Non-negative garrote threshold [2], [3]. It is intermediate betweenhardandsoftthresholding. It behaves like soft thresholding for small data values and approaches hard thresholding for large data values.In
greaterthresholding, the data is replaced with substitute where data is below the thresholding value. Greater data values pass untouched.In
lessthresholding, the data is replaced with substitute where data is above the thresholding value. Lesser data values pass untouched.Both
hardandsoftthresholding also support complex-valued data.- Parameters
- dataarray_like
Numeric data.
- valuescalar
Thresholding value.
- mode{‘soft’, ‘hard’, ‘garrote’, ‘greater’, ‘less’}
Decides the type of thresholding to be applied on input data. Default is ‘soft’.
- substitutefloat, optional
Substitute value (default: 0).
- Returns
- outputarray
Thresholded array.
See also
References
- 1
D.L. Donoho and I.M. Johnstone. Ideal Spatial Adaptation via Wavelet Shrinkage. Biometrika. Vol. 81, No. 3, pp.425-455, 1994. DOI:10.1093/biomet/81.3.425
- 2
L. Breiman. Better Subset Regression Using the Nonnegative Garrote. Technometrics, Vol. 37, pp. 373-384, 1995. DOI:10.2307/1269730
- 3
H-Y. Gao. Wavelet Shrinkage Denoising Using the Non-Negative Garrote. Journal of Computational and Graphical Statistics Vol. 7, No. 4, pp.469-488. 1998. DOI:10.1080/10618600.1998.10474789
Examples
>>> import numpy as np >>> import pywt >>> data = np.linspace(1, 4, 7) >>> data array([ 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([ 0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([ 0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([ 0. , 0. , 0. , 0.9 , 1.66666667, 2.35714286, 3. ]) >>> pywt.threshold(data, 2, 'greater') array([ 0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'less') array([ 1. , 1.5, 2. , 0. , 0. , 0. , 0. ])
- pywt.threshold_firm(data, value_low, value_high)#
Firm threshold.
The approach is intermediate between soft and hard thresholding [1]. It behaves the same as soft-thresholding for values below value_low and the same as hard-thresholding for values above thresh_high. For intermediate values, the thresholded value is in between that corresponding to soft or hard thresholding.
- Parameters
- dataarray-like
The data to threshold. This can be either real or complex-valued.
- value_lowfloat
Any values smaller then value_low will be set to zero.
- value_highfloat
Any values larger than value_high will not be modified.
- Returns
- val_newarray-like
The values after firm thresholding at the specified thresholds.
See also
Notes
This thresholding technique is also known as semi-soft thresholding [2].
For each value, x, in data. This function computes:
if np.abs(x) <= value_low: return 0 elif np.abs(x) > value_high: return x elif value_low < np.abs(x) and np.abs(x) <= value_high: return x * value_high * (1 - value_low/x)/(value_high - value_low)
firmis a continuous function (like soft thresholding), but is unbiased for large values (like hard thresholding).If
value_high == value_lowthis function becomes hard-thresholding. Ifvalue_highis infinity, this function becomes soft-thresholding.References
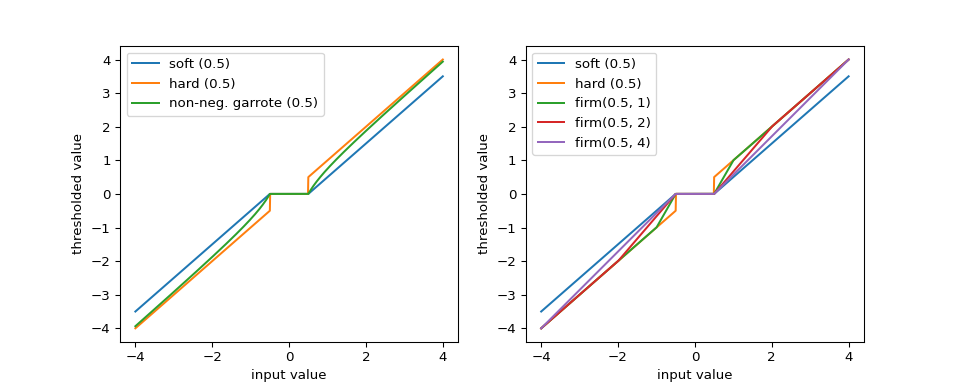
The left panel of the figure below illustrates that non-negative Garotte thresholding is intermediate between soft and hard thresholding. Firm thresholding transitions between soft and hard thresholding behavior. It requires a pair of threshold values that define the width of the transition region.
import matplotlib.pyplot as plt
import numpy as np
import pywt
s = np.linspace(-4, 4, 1000)
s_soft = pywt.threshold(s, value=0.5, mode='soft')
s_hard = pywt.threshold(s, value=0.5, mode='hard')
s_garrote = pywt.threshold(s, value=0.5, mode='garrote')
s_firm1 = pywt.threshold_firm(s, value_low=0.5, value_high=1)
s_firm2 = pywt.threshold_firm(s, value_low=0.5, value_high=2)
s_firm3 = pywt.threshold_firm(s, value_low=0.5, value_high=4)
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
ax[0].plot(s, s_soft)
ax[0].plot(s, s_hard)
ax[0].plot(s, s_garrote)
ax[0].legend(['soft (0.5)', 'hard (0.5)', 'non-neg. garrote (0.5)'])
ax[0].set_xlabel('input value')
ax[0].set_ylabel('thresholded value')
ax[1].plot(s, s_soft)
ax[1].plot(s, s_hard)
ax[1].plot(s, s_firm1)
ax[1].plot(s, s_firm2)
ax[1].plot(s, s_firm3)
ax[1].legend(['soft (0.5)', 'hard (0.5)', 'firm(0.5, 1)', 'firm(0.5, 2)',
'firm(0.5, 4)'])
ax[1].set_xlabel('input value')
ax[1].set_ylabel('thresholded value')
plt.show()